编辑:无损检测证书挂靠网 时间:2025-02-07 19:49:29
周国正(1986-),男,硕士,高级工程师,主要从事核电站燃料组件池边检查方面的研究
燃料棒是反应堆堆芯的关键部件,是放射性裂变产物的第一道屏障。相关研究表明,反应堆长时间运行后,包壳表面会发生腐蚀进而在外表面产生氧化膜。氧化膜的存在会严重影响包壳管的导热性能和燃料组件的热交换能力,带来安全风险。而且,随着氧化膜厚度的增加,燃料棒的温度会不断上升,加快腐蚀老化速度,影响燃料组件在堆内的使用寿命[1]。
氧化膜厚度是事关核电站运行安全的重要参数,有必要对其进行定期检测。涡流检测可直接在线定量测量出氧化膜厚度,同时具有检测速度快,不需要耦合剂,操作简便且成本低的优点。BECK等[2]研究了基于涡流提离效应的包壳氧化膜厚度测量探头的性能,验证了温度变化对氧化膜厚度的测量结果有较明显的影响。美国电力科学研究院(EPRI)YAGNIK等[3]研究了双频率测量方法,通过氧化膜厚度和剩余壁厚表征核燃料包壳的腐蚀情况,一定程度上提升了测量精度。美国电力科学研究院和意大利电子技术试验中心研究了基于多频测量技术和基于模型的测量数据分析方法,以量化核燃料包壳的氧化膜厚度。美国西屋公司ANDERSSON等则通过量化垢层的磁导率,一定程度上减小了磁性垢层对测量结果的影响。
现有检测方法在测量包壳管氧化膜厚度时,涂层厚度、包壳管电导率等参数的变化会带来测量值的波动,影响检测结果的准确性以及对燃料组件老化状态的准确评估。文章基于有限元仿真,首先对燃料棒包壳管涡流检测探头进行了参数优化;同时对影响氧化膜厚度测量的包壳管的电导率变化、金属涂层的厚度变化等进行了仿真分析;最后,利用多频测量技术,基于大量仿真数据集,进行多参数分离,抑制金属涂层厚度和包壳管电导率的影响,实现了氧化膜厚度的精确测量。
由频域的麦克斯韦方程及电磁场的本构关系计算推导可得到磁矢量势方程[4]
| (1) |
| (2) |
式中:ω,ν,σ分别为角频率,样品的磁阻率和电导率;A为磁矢势;V为电动势;Js为源电流密度。
为了提高氧化膜厚度测量仿真计算的准确性和速度,将磁矢量势A分成两个部分,即
| (3) |
式中:As为电流源引起的磁矢量势;Ar为包壳中感应电流引起的磁矢量势。
用Hs表示源电流引起的磁场强度,则有
| (4) |
将式(3)和(4)代入磁矢量势方程(1)和(2),可得到退行磁矢量势方程
| (5) |
| (6) |
式中:νr为相对磁阻率。
根据毕奥萨伐尔(Biot-Savart)定律,As和Hs分别为
| (7) |
| (8) |
式中:ν0为真空的磁阻率;μ0为真空磁导率;Ω′为电流源的体积;r和r′分别为待求解域和源电流域中的坐标。
线圈探头的输出电压信号幅值V为
| (9) |
式中:N为线圈的匝数;B为磁场强度;S为线圈的环绕区域;n为线圈所在平面的法向量方向向量;dl为源电流的微小线元素。
燃料棒包壳管多层结构的仿真模型如图1(a)所示。模型中包壳管材料为Zr合金,管道内直径为8.36 mm,外直径为9.50 mm,高度为32.00 mm。金属涂层包裹在包壳管外壁且与包壳管高度相同,为纯Cr材料。金属涂层外侧均匀包裹一层氧化膜。仿真过程中线圈紧贴氧化膜外壁且位于管道轴向方向中心,由于氧化膜为非导电介质,所以仿真模型中氧化膜厚度即可以理解为是线圈底部距离金属涂层的提离。包壳管有限元模型如图1(b)所示,包括包壳管样品及外围空气的有限元模型。为了保证仿真结果的准确性,并节约计算资源与时间,对六面体网格的大小进行了如下优化:沿z轴方向网格大小由中心位置向两边等比例增大;在xOy平面内,氧化膜结构为紧贴金属涂层的3层网格,其他网格则随着与氧化膜的周向距离等比例增大。包壳管外围空气体积设置足够大以减小边界效应。
线圈参数及有限元模型如图2所示。模型中将线圈沿周向方向切分为180个网格,选用线径为0.04 mm的线圈进行仿真,则线圈轴向方向网格数M和径向方向网格数N与实际匝数相近,可由式(10)和式(11)分别计算得到。仿真激励电流设置为5 mA。
| (10) |
| (11) |
式中:l为线圈高度;t为线圈厚度。
基于仿真模型,对4种外径(2.6,3.6,4.6,5.6 mm)、3种厚度(0.6,0.8,1.0 mm)和4种高度(0.3,0.5,0.7,1.0 mm)共48种不同尺寸的线圈进行了仿真分析,线圈激励频率为2.17 MHz。其仿真参数如表1所示。
| 项目 | 电导率(mS·m-1) | 相对磁导率 | 厚度/μm |
|---|---|---|---|
| 包壳管 | 1.43 | 1 | 570 |
| 金属涂层 | 7.57 | 1 | 15 |
| 氧化膜1 | 0 | 1 | 3 |
| 氧化膜2 | 0 | 1 | 7 |
定义Δ为去除模型中网格噪声的影响后,由线圈分别检测氧化膜厚度为3 μm和7 μm的样品时输出信号幅值的变化率,则有
| (12) |
式中:v3和v7分别为线圈检测氧化膜为3 μm和7 μm的输出信号幅值;v30和v70分别为线圈在具有相同网格模型的空气中所得的输出信号幅值。
不同尺寸线圈测量氧化膜厚度时的变化率仿真结果如表2所示,可得变化率Δ与线圈高度呈负相关;当线圈外径不小于3.6 mm时,变化率Δ与厚度呈正相关并与外径呈负相关。在表2参数中,外径为4.6 mm,厚度为1.0 mm,高度为0.3 mm的线圈对氧化膜厚度变化最敏感。因此,在接下来的仿真分析中,使用该参数的线圈。
| 外径/mm | 厚度/mm | 高度/mm | Δ/% | 外径/mm | 厚度/mm | 高度/mm | Δ/% |
|---|---|---|---|---|---|---|---|
| 2.6 | 0.6 | 0.3 | 0.098 | 4.6 | 0.6 | 0.3 | 0.109 |
| 0.5 | 0.084 | 0.5 | 0.100 | ||||
| 0.7 | 0.073 | 0.7 | 0.089 | ||||
| 1.0 | 0.061 | 1.0 | 0.077 | ||||
| 0.8 | 0.3 | 0.099 | 0.8 | 0.3 | 0.117 | ||
| 0.5 | 0.084 | 0.5 | 0.106 | ||||
| 0.7 | 0.072 | 0.7 | 0.096 | ||||
| 1.0 | 0.060 | 1.0 | 0.084 | ||||
| 1.0 | 0.3 | 0.098 | 1.0 | 0.3 | 0.124 | ||
| 0.5 | 0.083 | 0.5 | 0.111 | ||||
| 0.7 | 0.071 | 0.7 | 0.100 | ||||
| 1.0 | 0.059 | 1.0 | 0.087 | ||||
| 3.6 | 0.6 | 0.3 | 0.112 | 5.6 | 0.6 | 0.3 | 0.100 |
| 0.5 | 0.100 | 0.5 | 0.092 | ||||
| 0.7 | 0.089 | 0.7 | 0.086 | ||||
| 1.0 | 0.077 | 1.0 | 0.077 | ||||
| 0.8 | 0.3 | 0.118 | 0.8 | 0.3 | 0.108 | ||
| 0.5 | 0.104 | 0.5 | 0.099 | ||||
| 0.7 | 0.093 | 0.7 | 0.091 | ||||
| 1.0 | 0.079 | 1.0 | 0.082 | ||||
| 1.0 | 0.3 | 0.123 | 1.0 | 0.3 | 0.115 | ||
| 0.5 | 0.107 | 0.5 | 0.105 | ||||
| 0.7 | 0.095 | 0.7 | 0.096 | ||||
| 1.0 | 0.080 | 1.0 | 0.086 |
通过仿真分析了不同包壳管电导率对线圈输出信号幅值的影响,仿真参数如表3所示。
| 项目 | 电导率/(mS·m-1) | 相对磁导率 | 厚度/μm |
|---|---|---|---|
| 包壳管1 | 0.805 | 1 | 570 |
| 包壳管2 | 1.43 | 1 | 570 |
| 金属涂层 | 7.57 | 1 | 15 |
| 氧化膜1 | 0 | 1 | 3 |
| 氧化膜2 | 0 | 1 | 5 |
| 氧化膜3 | 0 | 1 | 7 |
| 氧化膜4 | 0 | 1 | 9 |
分别仿真了3种激励频率(1.00,2.17,4.75 MHz)、2种包壳管电导率(0.805,1.430 mS·m-1)条件下,线圈输出信号幅值随着氧化膜厚度变化的关系曲线,结果如图3所示,可以看出,线圈输出信号幅值随包壳厚度的增加而减小。
定义Δσ来量化包壳管电导率对线圈输出信号幅值的影响,则有
| (13) |
式中: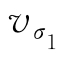 和
和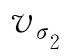 分别为电导率为0.805 mS·m-1和1.43 mS·m-1时线圈的输出信号幅值;
分别为电导率为0.805 mS·m-1和1.43 mS·m-1时线圈的输出信号幅值;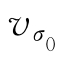 为相同网格时空气中线圈的输出信号幅值。
为相同网格时空气中线圈的输出信号幅值。
Δσ随激励频率增大的变化曲线如图4所示,可见包壳管电导率变化对线圈输出信号幅值的影响(Δσ)不超过0.7 %,激励频率越大,Δσ越小,即包壳管电导率对线圈输出信号幅值影响越小。这是因为激励频率越高,趋肤深度越小,包壳管电导率的变化对线圈电压的影响越小。
通过仿真研究分析了包壳管外不同金属涂层厚度对线圈输出信号幅值的影响,仿真参数如表4所示。
| 项目 | 电导率/(mS·m-1) | 相对磁导率 | 厚度/μm |
|---|---|---|---|
| 包壳管 | 1.43 | 1 | 570 |
| 金属涂层 | 7.57 | 1 | 6~20 |
| 氧化膜1 | 0 | 1 | 3 |
| 氧化膜2 | 0 | 1 | 7 |
分别仿真了3种激励频率(1.00,2.17,4.75 MHz)、2种氧化膜厚度(3,7 μm)条件下,线圈输出信号幅值随金属涂层厚度变化的关系曲线,结果如图5所示,可以看出,线圈输出信号幅值与金属涂层厚度、激励频率呈正相关,氧化膜厚度越大输出信号幅值越小。
通过仿真研究了氧化膜厚度变化对线圈输出信号幅值的影响,仿真参数如表5所示。
| 项目 | 电导率/(mS·m-1) | 相对磁导率 | 厚度/μm |
|---|---|---|---|
| 包壳管 | 1.43 | 1 | 570 |
| 金属涂层 | 7.57 | 1 | 15 |
| 氧化膜 | 0 | 1 | 3~8 |
线圈输出信号幅值随氧化膜厚度变化的关系曲线如图6所示。根据式(12)可计算出,激励频率分别为1.00,2.17,4.75 MHz时,氧化膜厚度为3 μm和7 μm的变化率(Δ)分别为0.111 1 %, 0.124 0 %和0.135 2 %。即,随着激励频率增高,线圈对于氧化膜厚度的变化更敏感。
多频多参数涡流检测技术将多个频率的激励信号作用在同一检测探头上,采用多参数分离的方式来消除多因素的干扰,提取有效的特征参数,该方法能够有效地抑制多种因素的干扰,提高涡流检测的效率。多频仿真参数设置如表6所示,其中频率采用对数形式,起始频率为0.4 MHz,终止频率为8.0 MHz,包括24个在频率轴上对数均匀分布的频率。
| 项目 | 电导率/(mS·m-1) | 相对磁导率 | 厚度/μm |
|---|---|---|---|
| 包壳管1 | 1.68 | 1 | 570 |
| 包壳管2 | 1.43 | 1 | 570 |
| 包壳管3 | 1.10 | 1 | 570 |
| 金属涂层1 | 7.57 | 1 | 6 |
| 金属涂层2 | 7.57 | 1 | 8 |
| 金属涂层3 | 7.57 | 1 | 10 |
| 金属涂层4 | 7.57 | 1 | 12 |
| 金属涂层5 | 7.57 | 1 | 15 |
| 金属涂层6 | 7.57 | 1 | 18 |
| 金属涂层7 | 7.57 | 1 | 20 |
| 氧化膜1 | 0 | 1 | 3 |
| 氧化膜2 | 0 | 1 | 5 |
| 氧化膜3 | 0 | 1 | 7 |
| 氧化膜4 | 0 | 1 | 9 |
包壳管电导率为1.43 mS·m-1,氧化膜厚度分别为3 μm和7 μm,金属涂层厚度为6,10,15,20 μm条件下,线圈输出信号幅值与激励频率的关系曲线如图7所示,可以看出,随着激励频率的增加,线圈输出信号幅值逐渐增大。
定义Δfo来量化不同频率下,线圈测量氧化膜厚度时的灵敏度,则有
| (14) |
式中: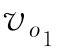 和
和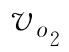 分别为氧化膜厚度为3 μm和7 μm时线圈的输出信号幅值;
分别为氧化膜厚度为3 μm和7 μm时线圈的输出信号幅值;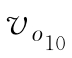 和
和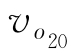 分别为氧化膜厚度为3 μm和7 μm时相同网格的空气模型中线圈输出信号幅值。
分别为氧化膜厚度为3 μm和7 μm时相同网格的空气模型中线圈输出信号幅值。
Δfo随着激励频率变化的曲线如图8所示。随着激励频率增大,涡流趋肤深度变小,同时金属涂层的增厚也会使涡流更加集中于包壳管表面的金属涂层中,而金属涂层的电导率大于包壳管电导率,线圈输出信号幅值更易受提离即氧化膜厚度的影响。反之,激励频率低或者金属涂层薄时,线圈输出还会受到包壳管材料的影响,因此其受到氧化膜厚度变化的影响相对更小。
假设氧化膜厚度h和线圈输出信号幅值X满足一个函数关系f(x)=h。其中X为二维数组,分别为多频激励下线圈输出信号幅值的实部、虚部。h与X的关系还会受到金属涂层厚度d和包壳管的电导率σ的影响。为了保证两者不影响氧化膜厚度测量结果,f还需对于d和σ的偏导均始终等于0。在实际问题中,很难将金属涂层厚度和包壳管电导率两者的影响完全去除,只能通过优化f,尽量降低两者对氧化膜测厚的影响。因此,在实际计算中,拟采用式(15)所示的优化方法来降低外部参数影响,并通过二次多项式拟合求解h和X的关系,最后将其用于其他样品的多频激励测量数据,就可以求解相应的氧化膜厚度。
| (15) |
基于非线性规划的优化思想,采用多起始点计算,即计算并比较多个起始点的值,以避免单个起始点陷入局部最优的情况,有助于获取全局最优解。该非线性规划算法在MATLAB环境中执行。
以包壳管电导率为1.25 mS·m-1为例,构建金属涂层d分别为7,13,14,17,19 μm的样品仿真模型,包壳管电导率等其他参数同理。分别计算上述24个激励频率下线圈测量氧化膜厚度h为2~10 μm的输出信号幅值。将输出信号幅值代入已知的函数关系中,计算相应的氧化膜厚度h′,结果如表7所示,可见,氧化膜厚度计算的绝对误差|h′-h|平均值为0.220 7 μm,最大值小于1 μm。
| h | d | ||||
|---|---|---|---|---|---|
| 7 | 13 | 14 | 17 | 19 | |
| 2 | 2.331 2 | 2.274 3 | 2.190 9 | 2.058 8 | 1.741 1 |
| 3 | 3.359 0 | 3.181 5 | 3.295 1 | 3.137 9 | 2.979 8 |
| 4 | 4.406 3 | 4.255 2 | 4.206 3 | 4.107 2 | 3.840 8 |
| 5 | 5.339 7 | 5.218 1 | 5.322 1 | 5.087 3 | 4.810 9 |
| 6 | 6.441 9 | 6.221 9 | 6.250 6 | 6.187 5 | 5.704 4 |
| 7 | 7.224 8 | 7.280 6 | 7.229 1 | 7.012 3 | 6.882 6 |
| 8 | 8.360 8 | 8.243 5 | 8.296 4 | 8.080 3 | 7.991 3 |
| 9 | 9.242 9 | 9.264 7 | 9.332 5 | 9.095 8 | 8.855 7 |
| 10 | 10.321 0 | 10.266 5 | 10.268 1 | 10.109 4 | 9.764 5 |
根据以上仿真结果,制备燃料棒包壳管氧化膜厚度测量探头,其实物如图9所示。该探头由两个线圈和一个陶瓷骨架组成,两个线圈分别固定在陶瓷骨架两侧。在测量过程中,靠近燃料棒表面的线圈为测量线圈,远离燃料棒表面的线圈为参考线圈。为了避免两个线圈参数不同而引起的误差,测量线圈与参考线圈各参数保持一致,其内径为4.0 mm、外径为5.6 mm、高度为0.5 mm,两个线圈间距为3.0 mm。测量系统整体结构示意如图10所示,其信号发生模块提供激励信号,测量探头贴近样品进行测量,与参考探头的信号进行差分放大,得到的信号进入信号处理系统进行处理,处理后的信号最终存储并显示在计算机上。
试验仪器为实验室自研的涡流仪,其实物如图11所示。该仪器的主要参数如下:激励频率为100 Hz~8 MHz;频率分辨率为1 Hz;激励电压为0~10 V;采样分辨率为16位;采样率为125 MHz·s-1;多频检测频率个数为4;地址信号为256个。试验参数设置与仿真参数保持一致。检测对象是直径为14 mm的锆合金核燃料包壳管,通过千分尺调节探头与燃料包壳管之间的距离(用来模拟氧化膜厚度),如图12所示。首先在0~100 μm内对探头做了标定,然后分别对30,20,10,0 μm的间距进行测量,得到测量结果如表8所示。其中实际值为千分尺的读数,测量值为试验系统测量得到的厚度间距值,可见,该组试验的测量绝对误差小于1 μm。
| 实际值 | 30 | 20 | 10 | 0 |
|---|---|---|---|---|
| 测量值 | 29.98 | 20.65 | 9.67 | 0.67 |
| 误差 | 0.02 | 0.65 | 0.33 | 0.67 |
文章研究了基于多频涡流检测技术精确测量氧化膜厚度的方法。试验结果表明,利用多频融合技术,可抑制金属涂层厚度和包壳电导率的影响,氧化膜厚度计算的绝对误差平均值为0.220 7 μm,且最大误差不超过1 μm,其他包壳管电导率条件下的结果相近。通过试验验证了测量系统的可行性,试验测量误差与仿真结果相近。
推荐阅读: