编辑:无损检测证书挂靠网 时间:2025-03-26 20:18:08
孙尔雁(1983—),男,硕士,副研究员,主要从事核燃料组件X射线成像技术和缺陷人工智能识别算法的研究工作
CT断层扫描技术是无损检测领域的一个重要分支,主要通过X射线投影重建断层图像,进而分析检测物体内部的缺陷。最新的研究进展包括利用断层图像生成三维模型,以及采用人工智能技术进行自动滤波矫正和缺陷的识别与测量。CT图像重建技术主要包括经典的滤波反投影算法(FBP)[1-2]和迭代重建算法[3]。迭代重建算法进一步分为代数迭代重建算法(AIR)和基于人工智能的统计迭代算法(MLEM)[4-6]。
与新兴的迭代算法相比,经典的FBP算法在计算效率上更高,尤其适合处理大型数据集或用于实时成像。其理论基础简洁明了,易于理解和实施,且对计算机GPU(图形处理器)的依赖较低。在数据质量良好且噪声水平较低的情况下,FBP算法能够生成高质量的图像。
滤波反投影算法的发展可以追溯到20世纪70~80年代。CORMACK和HOUNSFIELD[7-9]是CT技术的先驱,他们不仅提出了CT扫描的基本概念,还开发了其核心理论。CORMACK提出了投影切片定理,为CT图像重建提供了理论基础。HOUNSFIELD则发明了第一台实用的CT扫描仪。同时,滤波反投影算法的数学基础Radon变换,由JOHANN RADON在1917年提出。
在滤波函数的研究方面,Shepp和Logan于1974年提出了Shepp-Logan滤波器[10],这是一种理想的低通滤波器,专门用于降低投影数据中的高频噪声并改善图像质量。此外,其他重要的滤波器如Ram-Lak、Butterworth[11]、Hann和Hamming[12]滤波器也在CT图像重建中得到广泛应用。
迭代算法则通过建立像素与射线投影数据之间的关系系统矩阵,再进行迭代计算,来调整像素密度值以达到与试验测量数据的最佳匹配。这种算法在处理复杂物件时通常需要更高的GPU性能。
笔者基于计算机模拟试验的方法研究了几种滤波方法对CT成像质量的影响,旨在为CT重建图像质量的优化提供了一些参考。继续研究和优化基于滤波反投影算法的滤波功能和降噪技术,对于降低系统的计算需求具有重要意义。
Radon变换(见图1)是滤波反投影算法的数学基础,用于将二维灰度图像f(x,y)转换为投影数据R(t,θ)。这里,x和y是笛卡尔坐标系中的坐标,而R(t,θ)模拟探测器采集的数据,(t,θ)是对应的极坐标,反映了X射线通过被检测物体时的衰减情况。在此坐标系中,θ为新的投影坐标系(s,t)相对于(x,y)的旋转角度,而t是与X射线垂直的坐标。
Radon变换的定义式为
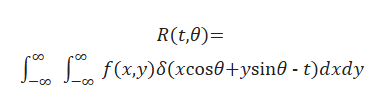
式中:δ为狄拉克函数,只在
迭代算法通过多次使用Radon变换来更新图像密度,从而生成新的投影数据。滤波反投影算法则主要利用反Radon变换。通过对投影数据R(t,θ)进行傅里叶变换得到频域函数P(ω,θ),然后与滤波函数进行卷积,即

式中:j为虚数单位;e为自然对数的底。
滤波后的投影数据g(t,θ)通过反投影来重建灰度图像f(x,y),即
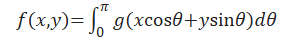
式中:|ω|为Ram-Lak滤波器,在频率域中增强高频信息,而高频成分通常代表图像中的边缘信息。
因此,滤波后的投影数据中的高频成分会增强图像的边缘特征,有助于保持图像的边缘清晰度。
根据奈奎斯特-香农采样定理[13],能够解析的最高空间频率是采样频率的一半。如果每个投影包含Nray个采样点,那么投影的空间频率W和频率步长e可以通过以下公式计算,即
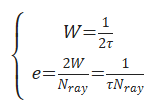
式中:τ为采样间隔。
两个连续投影之间的角增量σ可由180°总扫描角度除以投影数Mproj计算得出。由此,空间域和频域分辨率应相匹配以保持成像质量,即

由此可得投影数目与探测器像素之间的关系
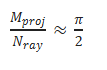
笔者对上述滤波反投影成像算法连续积分形式进行了离散近似,对滤波器和反投影步骤的数值实现进行了程序设计和计算研究。标准Shepp-Logan phantom幻影灰度图(350×350)和正弦图如图2所示,其中Nray=400,Mproj=628。
Ramp滤波器是滤波反投影图像重建算法中常用的一种滤波器,在频域中具有线性增长的特性,用于补偿反投影过程中的模糊效应。Ramp滤波器在数学上可以通过其频域和时(空)域来理解。
在频域中,Ramp滤波器可以表示为一个与频率呈线性关系的函数。设f为频率,Ramp滤波器的幅度可以表达为
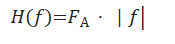
式中:FA为增益系数。
这意味着在频域中,滤波器的幅度与频率的绝对值成正比,从而对高频成分给予更高的权重。在空域中,Ramp滤波器的形式可以通过对其频域形式进行傅里叶逆变换得到[1]。理想情况下,Ramp滤波器的空域形式是一个奇异函数,其中心处有一个无限大的峰值,并且在远离中心的位置快速衰减。在滤波反投影法的图像重建中,Ramp滤波器对Radon变换后的投影数据进行卷积滤波后,再进行反投影重建。
Ramp滤波器的离散近似实现需要考虑到噪声放大和边缘效应。在实际应用中,还会配合采用窗函数(如汉宁窗或汉明窗)来减少噪声的影响。此外,由于Ramp滤波器在空域中是不局限的,其需要在有限长度的离散实线中被适当地截断和归一化。Ramp滤波器空域奇异函数的离散图如图3所示,图中横坐标表示离散空间索引n,n是一个整数序列,用于描述离散信号在空间上的位置,纵坐标表示奇异函数在对应时间点n的值,用h[n]表示,即滤波器中激响应值。
Ramp滤波器的构造过程可通过程序设计实现。
Ramp滤波器归一化频率f的坐标离散图如图4所示,其中在Nray取值的前200条投影对应的f取值为0~0.5,200~400条投影对应的f取值为-0.5~0。基于此坐标所构造的Ramp滤波函数H(f)离散图如图5所示,可见Ramp滤波函数的目的是在频域内加强高频成分的表现。
FA作为Ramp滤波函数的增益表现,本质上是投影数据的整体向高频部分漂移的程度。不同被检测物体的CT成像质量会受此增益系数的影响,因此在做滤波器设计时,需要寻找使成像质量最优化的增益系数。实际上,增益系数过高,投影数据的整体被加强的同时,噪声信号也会得到同样的增益。
Ramp滤波器滤波后成像结果与原始图形的比较如图6所示。
计算机断层扫描(CT)成像领域,影像质量的评估是一个重要环节。质量评估通常涉及多个方面,包括图像的清晰度、对比度、噪声水平、伪影等。评估CT图像质量的常用方法包括均方误差(MSE)、峰值信噪比(PSNR)、结构相似性指数(SSIM,图像完全相同时为1)、以及边缘保持指数(EPI)等[14],各方法对图6中所示的两张图分别做了评估,各指标及其随增益系数的变化情况如表1所示。
| 评价指标 | 增益系数FA | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| MSE | 0.02 | 0.01 | 0.01 | 0.04 |
| PSNR | 16.17 | 20.56 | 18.29 | 13.74 |
| SSIM | 0.41 | 0.55 | 0.57 | 0.54 |
| EPI | 124.66 | 257.99 | 373.19 | 225.61 |
表1显示,增益系数为3时,均方误差(MSE)达到最小,峰值信噪比(PSNR)则是在增益系数为2时达到峰值,其他两个评价指标也分别在增益系数为3时达到峰值。
Ramp滤波器的增益系数随频率增加而线性增加,导致了图像的高频信息(通常对应于图像边缘和细节)被强化。尽管这种增强可以提升图像的锐度和边缘清晰度,但在图像信号处理中,噪声通常也表现为高频成分。高频处的噪声同样被放大,这可能会导致图像中出现更多的噪声。因为X射线成像往往伴随着固有的噪声,所以CT成像中,这种噪声放大现象更加明显,笔者对滤波函数进行取幂操作,操作时,幂指数取1.5。取幂操作片面增强了高频信号,噪声成分凸显,基于归一化频率的Ramp滤波器成像结果如图7所示,直观上看,图像已经出现伪影,而其峰值信噪比PSNR降低到了14.4,相似性指标SSIM降低到了0.31,但边缘保持性指数EPI高达294。可见高频信号的片面加强,既增益了边缘保持性,也增益了噪声信号。加强高频信息,中低频的对比度相对降低,就会导致图像的低对比度区域在视觉上变得更难以分辨。Ramp滤波器的不合理设计还可能会导致图像的自然质地被过度强调或扭曲,影响图像的自然外观。
由于Ramp滤波器并不能同时良好地处理高低频信号,因此还需要在使用Ramp滤波后,进一步进行低通滤波或平滑处理,来调整高频放大的程度,以减少噪声并抑制伪影。Shepp-Logan滤波器是一种理想的低通滤波器,用于在投影数据域中滤除高频噪声,并改善重建图像的质量,通过sin c函数来修正Ramp滤波器,以减少噪声的放大。在频域中,Shepp-Logan滤波器的频率响应H(ω)由Ramp滤波器的频率响应和一个窗函数的乘积给出,即
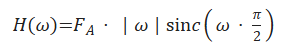
其中的窗函数定义为
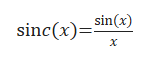
按sin c函数的定义,x=0其值为1[sin c(0)=1],其作用是减少高频增益的幅度,在图像边缘锐化和可允许的噪声范围内,获得二者的平衡,同时相应地增强低频信号,其成像结果如图8所示。
Shepp-Logan滤波器成像质量各评价指标的对比及其随增益系数的变化情况如表2所示,可见,成像质量最优处在于增益系数FA为1或2附近。但整体EPI值太低,意味着Shepp-Logan滤波器边缘保持性受到严重削弱,为此,笔者对该滤波器做了修正,修正后的结果如表3所示。
| 评价指标 | 增益系数 FA | |||
|---|---|---|---|---|
| 0.5 | 1 | 2 | 3 | |
| MSE | 0.04 | 0.02 | 0.01 | 0.02 |
| PSNR | 13.99 | 16.08 | 19.71 | 18.11 |
| SSIM | 0.34 | 0.41 | 0.54 | 0.57 |
| EPI | 87.19 | 102.66 | 83.51 | 62.61 |
| 评价指标 | FA | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| MSE | 0.02 | 0.01 | 0.01 | 0.04 |
| PSNR | 16.16 | 20.53 | 18.29 | 13.75 |
| SSIM | 0.41 | 0.55 | 0.58 | 0.55 |
| EPI | 121.82 | 242.92 | 352.14 | 228.39 |
改进后的Shepp-Logan滤波器公式为
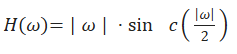
Shepp-Logan修正滤波器可通过程序设计实现,其中用Filter_Amplitude表示Shepp-Logan修正滤波函数的增益系数,由于f是归一化的频率坐标,不同被检测物品CT成像的质量会受此增益系数的影响,因此在做滤波器设计时,需要寻找使成像质量优化的增益系数。Shepp-Logan修正滤波器滤波后成像结果与原始图形的比较如图9所示。
由表3可见,当增益系数FA达到3时,各评价指标均达到最优,这一点和Ramp滤波器类似,因为Shepp-Logan修正滤波器本质上是在Ramp滤波器的基础上加窗构造而成的。修正的Shepp-Logan滤波器整体评价指标均有所提升,EPI值达到352,在兼顾了合适峰值信噪比的前提下,图像边缘保持性得到了显著的提升。
关于Shepp-Logan标准幻影图的成像,不同投影数目对成像质量,笔者开展了相应的计算机数值模拟研究的影响。成像质量研究的模拟结果如图10所示,其中,模拟探测器的采样数目Nray为400,投影数目为50~900。其中,幻影成像图由上到下,对应的投影数目依次为900,800,700,628,600,400,200,100,50。
成像算法所采用的滤波器为Ramp滤波器,增益系数FA=3,标准幻影的像素尺寸为400×400(长×宽)。由组图10可以看出,当所采集的投影数目降低至一定程度时,条状伪影开始显现;投影数目降低到100时,重建后图像的伪影开始肉眼可辨,降低到50时,重叠失真的情况已经十分明显了。
但通过评估指标测量图像质量,可以发现,当投影数目低于628时,各成像质量指标开始出现较为显著的衰减。其中均方误差(MSE)和结构相似性指数(SSIM)随投影数目的变化曲线如图11所示,峰值信噪比(PSNR)随投影数目的变化曲线如图12所示,边缘保持指数(EPI)随投影数目的变化曲线如图13所示。从图11~13中还可以看出,当投影数目超过628时,图像质量评价指标基本趋向于峰值,即便投影数目增加到900,对图像质量的增益效果也很微弱。计算机模拟研究进一步说明所推导的投影数目为探测器采样数目的1.57倍时是投影成像的最优点。
着重研究了滤波器和投影数目对投影质量的影响。Ramp滤波器是高频滤波器,其对高频信号的增益,增强了图像的边缘保持性指标,使得图像在不同密度边缘处更加清晰。但对于噪声干扰更大的情况,如高能X射线成像问题,就需要着重考虑高频信号增益所带来的负面效应。Shepp-Logan滤波器通过对Ramp滤波器进行一定程度地加窗,对高频信号增益效果进行了有效的抑制。但这种高频增益的抑制又会导致边缘保持性系数过小,并没有同时兼顾抑制噪声和边缘增益两种目的。
对Shepp-Logan滤波器进行了修正,新修正Shepp-Logan滤波器的成像结果的各方面评价指标都优于原来的滤波器和Ramp滤波器指标。究其原因在于修正的滤波器的窗函数更加平滑。文章还开展了扫描投影数目与伪影产生之间关联情况的计算机模拟试验,进一步论证了奈奎斯特-香农采样定理在CT成像算法中的实用性,图像空间信号投影数目的过度采集对于提高成像质量并没有增益性。
此外,经过分析发现滤波后投影数据的角积分,是所在的笛卡尔坐标平面上点(x,y)与原点距离作为直径的圆的线密度积分。据此发现,还可以引入GA遗传算法作为开发局部滤波反投影成像算法的理论依据。这对于复杂矩阵的成像计算,进一步降低对计算机算力资源的依赖,具有重要意义。